Similólúwa Òkunọwọ
Back to blog
•
9 min read
#Priority Queues#Go#Data Structures
Demystifying Priority Queues And Their Applications in Go

Demystifying Priority Queues And Their Applications in Go

Introduction to the priority queue data structure, implementation, and applications in Go

Introduction

Stacks and Queues are fundamental linear data structures in computer science that use the LIFO (Last In First Out) and FIFO (First In First Out) principle respectively for insertion and deletion of elements. In this article, we will delve into a special kind of Queue, known as a Priority Queue, to understand its implementation and applications using the Go programming language.

Who Is This Article For?

  • Beginners looking to explore basic data structures, implementation, and applications with Go.

Pre-Requisites

  • Go installed on Linux, Windows, or Mac
  • Foundational Go programming knowledge
  • Basic knowledge of Stack and Queues
  • A text editor or IDE (i.e. VSCode, Go Playground )

Learning Objectives

  • Brief Introduction to Priority Queues
  • Implementation of Priority Queues using arrays and linked lists in Go
  • Applications of Priority Queues: Implementing the Dijkstra algorithm using a Priority Queue

Overview of Priority Queues

A Priority Queue is a special kind of Queue that satisfies the following conditions: -

  • A priority is assigned to each element in the queue,
  • Insertion and Deletion operations in the queue are performed based on the order of priority,
  • If two elements in the queue have the same priority, they are de-queued following the FIFO principle.

Let’s assume you have a list of tasks to complete with associated priorities based on their deadlines, you want to ensure that the task with the highest priority is completed first to avoid missing your deadlines. Hence, the task with the highest priority is completed first (i.e. de-queued from the task queue). This is analogous to the operation of a generic priority queue.

Priority queues can be defined based on their type and mode of implementation. The main priority queue types are the Max-priority queue and the Min-priority queue. In a Max-priority queue, the element with the highest priority is removed/de-queued first, and conversely, the element with the least priority is de-queued first in a Min-priority queue.

Operations On A Priority Queue

The following operations are commonly implemented in a Priority Queue: -

  • isEmpty() - Checks if the priority queue is empty or not,
  • enqueue() or insert() - Inserts a new element into the priority queue based on the priority order
  • dequeue() or remove() - Removes and returns the element with the max/min priority from the priority queue,
  • peek() - Returns the element with the max/min priority from the priority queue,
  • length() - Returns the length or size of the priority queue.

Other operations can be added to the priority queue based on your use case and implementation.

Implementation Of A Priority Queue

Priority Queues can be implemented using several common data structures i.e. Arrays, Linked lists, and Binary heaps. Arrays and Linked lists are commonly used in simpler implementations to understand priority queues, while Binary heaps are used in more efficient implementations. In this article, we shall consider only the array and linked-list implementations for simplicity, however, this will provide an good foundation to help you understand more complex and efficient implementations.

The table below outlines the performance of different implementations of a priority queue using the Big-O notation: -

Implementation/ OperationUnsorted ArraySorted ArrayLinked ListBinary Heap
insert()O(1)O(n)O(n)O(log(n))
remove()O(n)O(1)O(1)O(log(n))
peek()O(n)O(1)O(1)O(1)

Implementation Of A Priority Queue In Go

In this section, we shall implement a priority queue in Go using an unsorted array, sorted array, and a singly-linked list.

To get started, let us define the types for the PriorityQueue and QueueElement using a struct.

package main
import (
	"fmt"
)

type QueueElement struct {
	value    interface{}
	priority int
}

type PriorityQueue struct {
	maxSize int
	data    []QueueElement
	size    int
}
// Sets the max-size of the priority queue
func (p *PriorityQueue) SetMaxSize(maxSize int) {
	p.maxSize = maxSize
}

// Checks if the priority queue is empty
func (p *PriorityQueue) IsEmpty() bool {
	return p.size == 0
}

// Display the elements of the queue in an array form
func (p *PriorityQueue) Display() {
	if p.IsEmpty() {
		panic("Queue is empty.")
	}
	arr := make([]interface{}, p.size)
	i := 0
    // Append each element in the priority queue to the array
	for i < p.size {
		arr[i] = p.data[i].value
		i++
	}
	fmt.Println("Priority Queue elements: ", arr)
}

The PriorityQueue type contains fields for maxSize, size, and a collection of the queue elements stored in the data array ([]QueueElement). The QueueElement type contains a value and an assigned priority as defined in the struct. The SetMaxSize() method sets the max size of the priority queue, the IsEmpty() method checks if the queue is empty, while the Display() method is used for displaying the values of the priority queue in an array form.

Using An Unsorted Array

An unsorted array is used to store the priority queue elements in this case. The enqueue()orinsert() operation inserts a new element at the end of the array irrespective of the priority order, this is performed in constant time i.e. O(1) time complexity. For the remove() or dequeue() operation, the array is searched for the max/min priority element which is removed and returned. The peek operation also performs the same search which takes linear time - O(n) time complexity.

This implementation is for a min-priority queue, hence the element with the smallest priority is removed first.

Code

//.... 
// Adds a new element to the priority queue (unsorted array case)
func (p *PriorityQueue) Enqueue(el interface{}, priority int) {
	newElement := QueueElement{el, priority}
	if p.size == p.maxSize {
		panic("Queue has reached its max size limit.")
	}

	p.data = append(p.data, newElement)
	p.size++
}

// Removes and returns the element with the min-priority from the PQ
func (p *PriorityQueue) Dequeue() QueueElement {
	if p.IsEmpty() {
		panic("Queue is empty.")
	}

	idx := 0
	// Traverse through the unsorted array to find the element with the smallest min-priority
	for i := 0; i < p.size; i++ {
		if p.data[i].priority < p.data[idx].priority {
			idx = i
		}
	}
	dequeuedEl := p.data[idx]
	// Remove the dequeued element from the PQ
	p.data = append(p.data[:idx], p.data[idx+1:]...)
	p.size--
	return dequeuedEl
}

// Peek (Returns the element with the min-priority from the PQ)
func (p *PriorityQueue) Peek() QueueElement {
	if p.IsEmpty() {
		panic("Queue is empty.")
	}
	dequeuedEl := p.data[0]
	// Traverse through the unsorted array to find the element with the min-priority
	for _, el := range p.data {
		if el.priority < dequeuedEl.priority {
			dequeuedEl = el
		}
	}
	return dequeuedEl
}

Testing

//...
func main(){
    pq := PriorityQueue{}
    pq.SetMaxSize(10)
    pq.Enqueue(1, 5)
    pq.Enqueue(5, 2)
    pq.Enqueue(6, 3)
    pq.Enqueue(10, 1)
    pq.Enqueue(8, 2)
    
    pq.Display()                          //Returns [1,5,6,10,8]
    fmt.Println(pq.Dequeue())   //Returns {10 1}
    fmt.Println(pq.Dequeue())   //Returns {5 2}
    fmt.Println(pq.Dequeue())   //Returns {8 2}
    fmt.Println(pq.Peek())          //Returns {6 3}
    pq.Display()                          //Displays [1,6]
}

The unsorted array implementation can be accessed HERE

Using A Sorted Array

A sorted array is used to store the priority queue elements. The enqueue() or insert() operation involves searching through the priority queue for the element’s right position based on the priority ordering scheme, this search is performed in linear time - O(n). The dequeue() or remove() operation simply involves removing and returning the top element from the array. This operation is performed in constant time - O(1) because the elements are already sorted in the order of priority. The peek() operation also takes constant time - O(1).

Code

// Adds a new element to the priority queue in its exact location
func (p *PriorityQueue) Enqueue(el interface{}, priority int) {
	newElement := QueueElement{el, priority}
	if p.size == p.maxSize {
		panic("Queue has reached its max size limit.")
	}
    // Append the new element if the PQ is empty
	if p.IsEmpty() {
		p.data = append(p.data, newElement)
		p.size++
		return
	}

	p.data = append(p.data, newElement)
	i := p.size - 1 
    // Search for the correct position of the new element by comparing priorities
	for i >= 0 {
		if p.data[i].priority > priority {
			p.data[i+1] = p.data[i]
			i--
		} else {
			break
		}
	}
	p.data[i+1] = newElement
	p.size++
}

// Returns and Removes the first element of the priority queue
func (p *PriorityQueue) Dequeue() QueueElement {
	if p.IsEmpty() {
		panic("Queue is empty.")
	}
	dequeued := p.data[0]
	p.data = p.data[1:]
	p.size--
	return dequeued
}

// Returns the first element in the queue without modifying the queue
func (p *PriorityQueue) Peek() interface{} {
	if p.IsEmpty() {
		panic("Queue is empty.")
	}
	return p.data[0]
}

Testing

//...
func main() {
	pq := PriorityQueue{}
	pq.SetMaxSize(10)
	pq.Enqueue(1, 5)
	pq.Enqueue(5, 2)
	pq.Enqueue(6, 3)
	pq.Enqueue(10, 1)
	pq.Enqueue(8, 2)

	pq.Display()                           //Returns [10,5,8,6,1]
	fmt.Println(pq.Dequeue())     //Returns {10 1}
	fmt.Println(pq.Dequeue())     //Returns {5 2}
	fmt.Println(pq.Dequeue())     //Returns {8 2}
	fmt.Println(pq.Peek())            //Returns {6 3}
	pq.Display()                            //Displays [1,6]
}

The sorted array implementation can be accessed HERE

Using A Linked List

A Linked list is a linear data structure consisting of nodes that contain a value and a reference (or link) to another node. Hence, elements in a linked list are not stored in contiguous memory locations. In the scope of this article, we shall implement a priority queue using a singly-linked list. The head of this linked-list will be the element with the min-priority, the enqueue() operation involves traversing the linked-list to find the right position to insert the new element based on the priority ordering.

This search and insertion process takes linear time - O(n). The dequeue() operation basically unlinks the head (min-priority element) from the linked list and returns it while the peek() operation returns the head of the linked list without modifying the linked-list. The dequeue() and peek() operations are performed in constant time.

Code

//...
// Struct Type definition for a Queue node
type QueueNode struct {
	value    interface{}
	priority int
	next     *QueueNode
}

// Struct Type definition for the Priority Queue
type PriorityQueue struct {
	head    *QueueNode
	maxSize int
	size    int
}

// Display elements of the Priority Queue in an array form
func (p *PriorityQueue) Display() {
	if p.IsEmpty() {
		panic("Queue is empty.")
	}
    
	arr := make([]interface{}, p.size)  // Create a new slice
	ptr := p.head 
    // Traverse through the linked-list and append each element to the array
	for i := 0; i < p.size && ptr != nil; i++ {
		arr[i] = ptr.value
		ptr = ptr.next
	}

	fmt.Println("Priority Queue: ", arr)
}

To implement the Enqueue(), Dequeue(), and Peek() methods: -

//...
// Enqueue operation, add a new element to the priority queue
func (p *PriorityQueue) Enqueue(el interface{}, priority int) {
	if p.size == p.maxSize {
		panic("Queue is full.")
	}
	newQueueNode := &QueueNode{}
	newQueueNode.value = el
	newQueueNode.priority = priority

	if p.IsEmpty() {
		p.head = newQueueNode
		p.size++
		return
	}

	ptr := p.head
    // Traverse through the linked-list to search for the correct position of the new element based on the priority
	if priority < p.head.priority {
        // Special case: If priority of the incoming element is less than that of the head node
		p.head = newQueueNode
		p.head.next = ptr
		p.size++
	} else {
		for i := 0; i < p.size && ptr.next != nil; i++ {
			if ptr.next.priority <= priority {
				ptr = ptr.next
				fmt.Println(ptr.value)
			}
		}

		temp := ptr.next
		ptr.next, newQueueNode.next = newQueueNode, temp
		p.size++
	}
}

// Dequeue operation
func (p *PriorityQueue) Dequeue() QueueNode {
	if p.IsEmpty() {
		panic("Queue is empty.")
	}
    // Dequeued element is the head node
	dequeued := *p.head
    // Un-link the head node from the linked-list
	if p.head.next != nil {
		p.head = p.head.next
	} else {
		p.head = nil
	}
	p.size--
	return dequeued
}

// Peek operation
func (p *PriorityQueue) Peek() QueueNode {
	if p.IsEmpty() {
		panic("Queue is empty.")
	}
    // Return the head node
	return *p.head
}

Testing

//...
func main() {
	pq := PriorityQueue{}
	pq.SetMaxSize(10)
	pq.Enqueue(1, 5)
	pq.Enqueue(5, 2)
	pq.Enqueue(6, 3)
	pq.Enqueue(10, 1)
	pq.Enqueue(8, 2)

	pq.Display()              //Returns [10,5,8,6,1]
	fmt.Println(pq.Dequeue()) //Returns {10 1 0xc000096040}
	fmt.Println(pq.Dequeue()) //Returns {5 2 0xc0000960a0}
	fmt.Println(pq.Dequeue()) //Returns {8 2 0xc000096060}
	fmt.Println(pq.Peek())    //Returns {6 3 0xc000096020}
	pq.Display()              //Displays [6,1]
}

The linked-list implementation can be accessed HERE

Awesome, Congratulations on coming so far. In this next section of this article, we shall explore several applications of the priority queue.

Practical Applications Of Priority Queues

There are a number of practical applications of priority queues applied in computing, operating systems, and implementing popular algorithms efficiently. Some of these applications include: -

Implementation Of Dijkstra Algorithm Using A Priority Queue

A graph is a non-linear data structure that consists of nodes/vertices which are interconnected via edges. For instance, social networks like Facebook, LinkedIn, Twitter, etc. can be modeled as graphs where the nodes represent people, and the edges connecting the nodes signify a relationship between the people in the network i.e. an edge connecting person A and person B might imply that person A is following person B.

The Dijkstra algorithm is an algorithm for computing the shortest path between nodes in a graph with positively weighted edges only i.e. finding the shortest route between two streets in Google maps. Let us consider the graph below, the nodes are represented with colored circles and the edges are represented with lines connecting the circles. The numbers assigned to the edges are called “weights” or “costs”, which signify the distance between the nodes in this case.

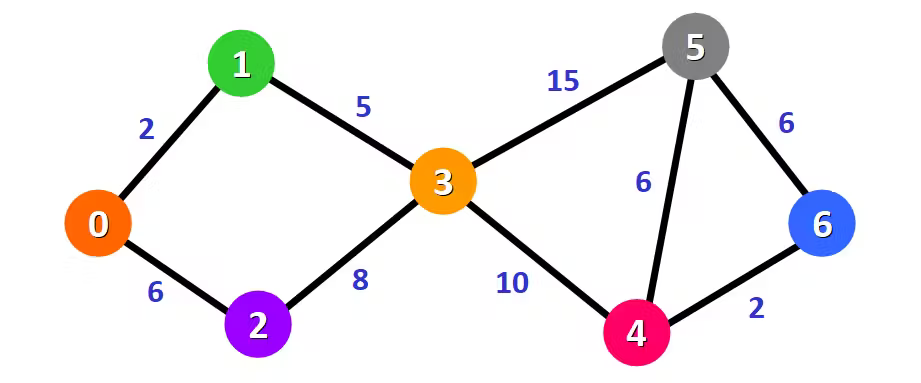
Illustration Of A Graph With Weighted Edges
Illustration Of A Graph With Weighted Edges
Source: https://www.freecodecamp.org/news/dijkstras-shortest-path-algorithm-visual-introduction/

The Dijkstra algorithm can be used to compute the shortest path from one vertex (i.e. 0) to other vertices in a graph.

The steps required to implement the Dijkstra algorithm using a Priority queue are: -

  1. Initialize the graph: Define a V x V adjacency matrix [1] to represent the graph and the edges, where V=number of vertices

    //...
type Graph struct {
    numVertices     int
    adjacencyMatrix [][]float64
}

// Initialize a V*V adjacency matrix for the new graph
func NewGraph(numVertices int) Graph {
    newGraph := Graph{}
    newGraph.numVertices = numVertices
    newGraph.adjacencyMatrix = make([][]float64, numVertices)
    for i := 0; i < numVertices; i++ {
        arr := make([]float64, numVertices)
        for i := 0; i < numVertices; i++ {
            arr[i] = -1
        }

        newGraph.adjacencyMatrix[i] = arr
    }

    return newGraph
}

// Add a new edge to the graph by updating the adjacency matrix
// For two adjacent vertices i and j, the matrix element M[i][j] = weight of the edge
func (p *Graph) addEdge(v1 int, v2 int, weight float64) {
    if v1 == v2 {
        panic("A Node cannot be connected to it self.")
    }
    p.adjacencyMatrix[v1][v2] = weight
    p.adjacencyMatrix[v2][v1] = weight
}

  2. Iteration: Select the unvisited vertex with the smallest distance (this will be done using the priority queue). The for each neighbor of the selected vertex, calculate the distance to between that neighbor and the current vertex. If the distance is less than the current distance to that neighbor, update the neighbor’s distance.

    The priority queue significantly improves the performance of this step by efficiently selecting the vertex with the smallest distance at each step.

  3. Termination: Repeat step 2 until all vertices have been visited or the destination vertex has been reached.

Code

// Dijkstra algorithm implementation for a graph
func (p *Graph) FindShortestPaths(v int) map[int]float64 {
	// Create an array to store visited vertices
	var visited []int
	// Create a map that stores the vertice and the corresponding distance
	// The initial distance from the start vertex is initialized to infinity for all vertices except the start vertex which is initialized to 0
	m := make(map[int]float64)
	for i := 0; i < p.numVertices; i++ {
		m[i] = math.Inf(0)
	}
	m[v] = 0
	// Initialize the priority queue
	q := PriorityQueue{}
	q.SetMaxSize(p.numVertices)
	q.Enqueue(float64(v), 0) // The distance is the priority
	for {
		if q.size <= 0 {
			break
		}
		dequeued := q.Dequeue()
		var distance float64
		distance = float64(dequeued.priority)
		currentVertex := dequeued.value.(float64)
		visited = append(visited, int(currentVertex))
		//fmt.Println("Visited: ", visited)
		for i := 0; i < p.numVertices; i++ {
			// Iterate through all the neighbor vertices
			if p.adjacencyMatrix[int(currentVertex)][i] != -1 {
				distance = p.adjacencyMatrix[int(currentVertex)][i]
				if !contains(visited, i) {
					oldDistance := m[i]
					newDistance := m[int(currentVertex)] + distance
					// Check if newDistance is greater than oldDistance
					// If true, enqueue the queue with the newDistance, and update the distance for that vertice in the map of vertices and distances
					if oldDistance > newDistance {
						q.Enqueue(float64(i), int(newDistance))
						m[i] = float64(newDistance)
					}
				}
			}
		}
	}

	//Display the shortest paths
	for i := 0; i < p.numVertices; i++ {
		if i != v {
			fmt.Printf("Shortest path between %d and %d = %d\n", v, i, int(m[i]))
		}
	}
	return m
}

// Utility function to check if a slice contains an element
func contains(s []int, el int) bool {
	var result bool = false
	for i := 0; i < len(s); i++ {
		if el == s[i] {
			result = true
			break
		}
	}

	return result
}

Testing

To test our implementation, we shall use the graph shown in the image above with seven vertices. We shall compute the shortest path from the 0 vertex: -

func main() {
	// Initialize the adjacency matrix with 7 vertices
	g := NewGraph(7)
	// Add the edges with their associated weights
	g.addEdge(0, 1, 2)
	g.addEdge(0, 2, 6)
	g.addEdge(1, 3, 5)
	g.addEdge(2, 3, 8)
	g.addEdge(3, 5, 15)
	g.addEdge(3, 4, 10)
	g.addEdge(4, 5, 6)
	g.addEdge(5, 6, 6)
	g.addEdge(4, 6, 2)
	fmt.Println(g.adjacencyMatrix)
    // Compute the shortest paths from vertex `0` using the Dijkstra algorithm
	fmt.Println(g.FindShortestPaths(0))
}

Result

[[-1 2 6 -1 -1 -1 -1] [2 -1 -1 5 -1 -1 -1] [6 -1 -1 8 -1 -1 -1] [-1 5 8 -1 10 15 -1] [-1 -1 -1 10 -1 6 2] [-1 -1 -1 15 6 -1 6] [-1 -1 -1 -1 2 6 -1]]
Shortest path between 0 and 1 = 2
Shortest path between 0 and 2 = 6
Shortest path between 0 and 3 = 7
Shortest path between 0 and 4 = 17
Shortest path between 0 and 5 = 22
Shortest path between 0 and 6 = 19
Program exited.

The code for the Dijkstra algorithm implementation with Priority queues can be accessed HERE.

Conclusion

Thank you for reading 💖, I hope you’ve learned useful concepts regarding priority queues and their applications. Kindly access the references below to explore priority queues and their applications in-depth.

References

Footnotes

  1. [1]
    An adjacency matrix is a square matrix that represents the connections between vertices in a graph, where a non-zero value in a cell indicates an edge between the corresponding vertices. While an adjacency matrix can be used, an adjacency list is often more efficient for graphs with fewer edges as shown in the example we implemented.
    ↩